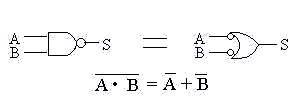
Teoremas da Álgebra de Boole
ATENÇÃO: A' significa NOT
( A ) ; B' significa NOT ( B )
Uma função combinacional pode ser
escrita de várias maneiras, sem ser alterada, fazendo-se uso dos Teoremas da Álgebra
de Boole. Por exemplo:
a) (A . B)' = A' + B'
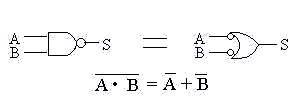
b) (A + B)' = A'. B'
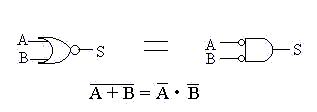
onde os símbolos " ' " e " + " representam :
a negação (NOT) e a função (OR)
respectivamente.
Aqui usou-se um teorema
conhecido como Teorema de De Morgan.
Os principais teoremas da Álgebra
Booleana são:
| Ordem | Teoremas | Ordem | Teoremas |
|---|---|---|---|
| 1 | A + 0 = A | 11 | A . B + A . B' = A |
| 2 | A + 1 = 1 | 12 | (A + B) . (A + B') = A |
| 3 | A + A = A | 13 | A + A' . B = A + B |
| 4 | A + A' = 1 | 14 | A . (A' + B) = A . B |
| 5 | A . 1 = A | 15 | A + B . C = (A + B) . (A + C) |
| 6 | A . 0 = 0 | 16 | A . (B + C) = A . B + A . C |
| 7 | A . A = A | 17 | A . B + A' . C = (A + C) . (A' + B) |
| 8 | A . A' = 0 | 18 | (A + B) . (A' + C) = A . C + A' . B |
| 9 | A + A . B = A | 19 | A . B + A' . C + B . C = A . B + A' . C |
| 10 | A . ( A + B) = A | 20 | (A + B) . (A' + C) . (B + C) = (A + B) . (A' + C) |
Como qualquer prova de teorema, a cada passo em direção à prova, você tem que dizer o porque do passo. Veja este exemplo (a prova do teorema 10):
A . (A + B)
= (pelo teorema 16)
A . A + A . B
= (teorema 7)
A + A . B
= (teorema 5)
A . 1 + A . B
= (teorema 16)
A . (1 + B)
= (teorema 2)
A . 1
= (teorema 5)
A
o que completa a prova. É muito importante
que você exercite este tipo de problema,uma vez que são absolutamente importantes para o
estudo de
Circuitos Digitais combinacionais.
Exercícios Resolvidos de Simplificação de funções lógicas :
1)
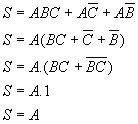
2)
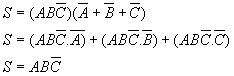
3)
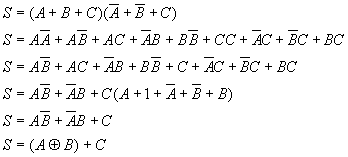
4)
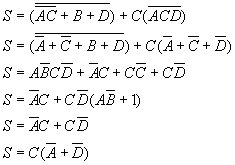
5)
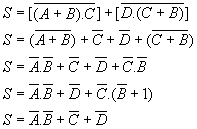
6)
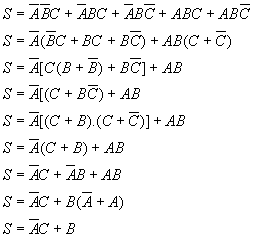
7)
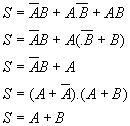
8)
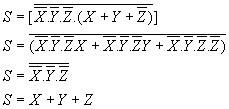
9)
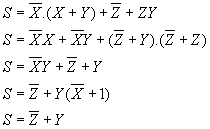
10)
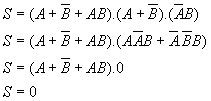
11)
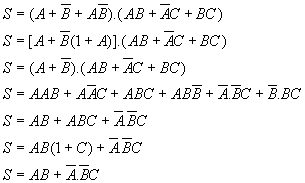
12)
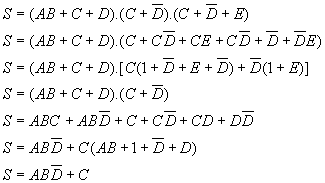
13)
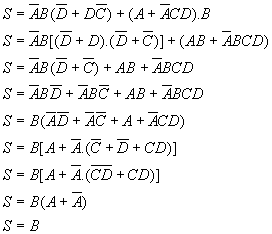
14)
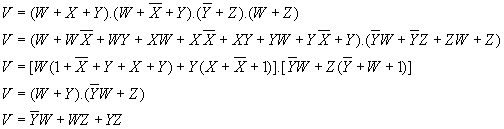
Técnica Soma de Produtos e Técnica Produto de Somas