SISTEMAS DE NUMERAÇÃO
Desde quando se começou a registrar informações sobre quantidades, foram criados diversos métodos de representar as quantidades.
O método ao qual estamos acostumados usa um sistema de numeração posicional. Isso significa que a posição ocupada por cada algarismo em um número altera seu valor de uma potência de 10 (na base 10) para cada casa à esquerda.
Por exemplo, no sistema decimal (base 10), no número 125 o algarismo 1 representa 100 (uma centena ou 102) , o 2 representa 20 (duas dezenas ou 2x101) e o 5 representa 5 mesmo (5 unidades ou 5x100). Assim, em nossa notação,
125 = 1x102 + 2x101 + 5x100
Base de um Sistema de Numeração
A base de um sistema é a quantidade de algarismos disponível na representação. A base 10 é hoje a mais usualmente empregada, embora não seja a única utilizada.
Os computadores utilizam a base 2 (sistema binário) e os programadores, por facilidade, usam em geral uma base que seja uma potência de 2, tal como 24 (base 16 ou sistema hexadecimal) ou eventualmente ainda 23 (base 8 ou sistema octal).
Na base 10, dispomos de 10 algarismos para a representação do número: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Na base 2, seriam apenas 2 algarismos: 0 e 1. Na base 16, seriam 16: os 10 algarismos aos quais estamos acostumados, mais os símbolos A, B, C, D, E e F, representando respectivamente 10, 11, 12, 13, 14 e 15 unidades. Generalizando, temos que uma base b qualquer é constituída de b algarismos, variando entre 0 e (b-1).
Generalizando, representamos uma quantidade N qualquer, numa dada base b, com um número tal como segue:
Nb = an.bn + .... + a2.b2 + a1.b1 + a0.b0 + a-1.b-1 + a-2.b-2 + .... + a-n.b-n sendo que
an.bn + .... + a2.b2 + a1.b1 + a0.b0 é a parte inteira e
a-1.b-1 + a-2.b-2 + .... + a-n.b-n é a parte fracionária.
Intuitivamente, sabemos que o maior número que podemos representar, com n algarismos, na base b, será o número composto n vezes pelo maior algarismo disponível naquela base (ou seja, b-1). Por exemplo, o maior número que pode ser representado na base 10 usando 3 algarismos será 999 (ou seja, 103 - 1 = 999).
Generalizando, podemos ver que o maior número inteiro N que pode ser representado, em uma dada base b, com n algarismos (n "casas"), será N = bn - 1. Assim, o maior número de 2 algarismos na base 16 será FF16 que, na base 10, equivale a 25510 = 162 - 1.
MUNDO
DIGITAL
Vivemos num mundo onde as grandezas presentes são analógicas,isto é,podem assumir qualquer valor numa faixa contínua de valores.Isto significa que qualquer tipo de ruído,seja qual for a sua origem,irá inevitavelmente alterar as variáveis e interferir nos dados apresentados.Para contornar esse problema,foram criados os circuitos digitais.
Os equipamentos que utilizam circuitos digitais, utilizam apenas o sistema binário, isto é, todas as informações armazenadas ou processadas nesses equipamentos usam apenas duas grandezas, representadas pelos algarismos 0 e 1.
Essa decisão de projeto deve-se à maior facilidade de representação interna no equipamento, que é obtida através de dois diferentes níveis de tensão,onde não importa o valor exato da tensão,mas sim uma faixa de tensões que caracterizam os níveis lógicos 0 (Low Level) e 1 (High Level). Havendo apenas dois algarismos, portanto dígitos binários, o elemento mínimo de informação nos equipamentos digitais é chamado de bit ( binary digit).
A base binária e a lógica criada por BOOLE possibilitaram a criação de circuitos denominados PORTAS LÓGICAS(elementos básicos para a invenção das máquinas digitais).
A origem da palavra DIGITAL vem justamente do fato de podermos contar com um só dedo(ou seja,um só dígito)os dois algarismos("0"e"1").
Representação Binária
Na base 2, o número "10" vale dois. Mas se 102 = 210, então dez é igual a dois?
NÃO, dez não é e nunca será igual a dois!
Na realidade, "10" não significa necessariamente
"dez". Nós estamos acostumados a associar "10" a "dez"
porque estamos acostumados a usar o sistema de numeração decimal. O número
102 seria lido "um-zero" na base 2 e vale 210 (convertido para "dois" na base dez),
105 seria lido "um-zero" na base 5 e vale 510 (convertido para "cinco" na base dez),
1010 pode ser lido como "um-zero" na base 10 ou
então como "dez" na base dez,
1016 seria lido "um-zero" na base 16 e vale 1610 (convertido para "dezesseis" na base dez), etc.
Portanto, 10 só será igual a dez se - e somente se - o número estiver representado na base dez!
OBS.: Toda vez que um número for apresentado sem que seja indicado em qual sistema de numeração ele está representado, a base numérica utilizada é decimal. Sempre que outra base for utilizada, a base será obrigatoriamente indicada.
Repr.Binária |
Potência |
Repr.Decimal |
| 1 | 20 | 1 |
| 10 | 21 | 2 |
| 100 | 22 | 4 |
| 1000 | 23 | 8 |
| 10000 | 24 | 16 |
| 100000 | 25 | 32 |
| 1000000 | 26 | 64 |
| 10000000 | 27 | 128 |
| 100000000 | 28 | 256 |
| 1000000000 | 29 | 512 |
| 10000000000 | 210 | 1.024 |
A representação binária é perfeitamente adequada para utilização pelos computadores
No entanto, um número representado em binário pode apresentar muitos bits, ficando longo e passível de erros quando manipulado por seres humanos normais como por exemplo os programadores, analistas e engenheiros de sistemas.
Para facilitar a visualização e manipulação dos dados e instruções processados em computadores, é usualmente adotada a representação hexadecimal (base 16). Ressaltamos mais uma vez que o computador opera apenas na base 2 e a representação hexadecimal não é usada no computador, ela se destina apenas à manipulação de grandezas pelos programadores.
Representação em Octal e em Hexadecimal
Para reduzir o número
de algarismos da representação e consequentemente facilitar a compreensão da grandeza e
evitar erros temos o sistema octal (base 8),onde cada três bits são representados por
apenas um algarismo octal (de 0 a 7), e o sistema hexadecimal (base 16),onde cada quatro
bits são representados por apenas um algarismo hexadecimal (de 0 a F ).
A seguir, apresentamos uma tabela com os números em decimal e sua representação correspondente em binário, octal e hexadecimal:
| Base 10 | Base 2 | Base 8 | Base 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Nota: a base 16 ou sistema hexadecimal pode ser indicada também por um "H" ou "h" após o número; por exemplo: FFH significa que o número FF está em hexadecimal. Não confundir o "H" ou "h" com mais um dígito, mesmo porque em hexadecimal só temos algarismos até "F".
Visualizando Base Binária e Base Hexadecimal
Conversões entre Bases
Vamos analisar agora as regras gerais para converter números entre duas bases
quaisquer.
Conversões entre as bases 2, 8 e 16
As conversões mais simples são as que envolvem bases que são potências entre
si. Vamos exemplificar com a conversão entre a base 2 e a base 8. Como 23 = 8, separando os bits de um número binário em grupos de tres
bits (começando sempre da direita para a esquerda!) e convertendo cada grupo de tres bits
para seu equivalente em octal, teremos a representação do número em octal. Por exemplo:
101010012 = 10 / 101 / 0012 (separando em grupos de 3, sempre começando da direita para a
esquerda)
Sabemos que 0102 = 28 ;
1012 = 58 ; 0012 = 18 portanto 101010012 = 2518
Vamos agora exemplificar com uma conversão entre as bases 2 e 16. Como 24 = 16, basta separarmos em grupos de 4 bits (começando sempre da direita para a esquerda!) e converter.
Por exemplo:
11001010111111102 = 1100
/ 1010 / 1111 / 11102 (separando em grupos de 4
bits, sempre começando da direita para a esquerda)
Sabemos que 11002 = C16;
10102 = A16 ; 11112 = F16 ; 11102
= E16
portanto 11001010111111102 = CAFE16
Vamos agora exercitar a conversão inversa. Quanto seria 3F5H (lembrar que o H está designando "hexadecimal") em octal? O método mais prático seria converter para binário e em seguida para octal.
3F5H = 11 / 1111 / 01012
(convertendo cada dígito hexadecimal em 4 dígitos binários) =
= 1 / 111 / 110 / 1012 (agrupando de tres em tres bits) =
= 17658 (convertendo cada grupo de tres bits para seu
valor equivalente em octal).
Conversão de Números em uma base b qualquer para a base
10
Vamos lembrar a expressão geral já apresentada:
Nb = an.bn + .... + a2.b2 + a1.b1 + a0.b0 + a-1.b-1 + a-2.b-2 + .... + a-n.b-n
A melhor forma de fazer a conversão é usando essa expressão. Tomando como exemplo o número 1011012, vamos calcular seu valor representado na base dez. Usando a expressão acima, fazemos:
1011012 = 1x25 + 0x24 + 1x23 + 1x22 + 0x21 + 1x20 = 32 + 0 + 8 + 4 + 0 + 1 = 4510
Podemos fazer a conversão de números em qualquer base para a base 10 usando o algoritmo acima.
Exemplos:
a) Converter 4F5H para a base 10 .
Solução: Lembramos que o H significa que a representação é hexadecimal (base 16).
Sabemos ainda que F16=1510.
Então:
4x162 + 15x161 + 5x160 = 4x256 + 15x16 + 5 = 1024 + 240 + 5 = 126910
b) Converter 34859 para a base
10.
Solução: 3x93 + 4x92 +
8x91 + 5x90 = 3x729 +
4x81 + 8x9 + 5 = 2187 + 324 + 72 + 5 = 258810.
c) Converter 1001,012 para a
base 10.
Solução: 1x23 + 0x22 +
0x21 + 1x20 + 0x2-1 + 1x2-2 = 8 + 0 + 0 + 1 + 0 +
0,25 = 9,2510
d) Converter 34,35 para a base
10.
Solução: 3x51 + 4x50 +
3x5-1 = 15 + 4 + 0,6 = 19,610
e) Converter 38,38 para a base
10.
Solução: Uma base b dispõe dos algarismos entre 0 e (b-1). Assim, a
base 8 dispõe dos algarismos 0 a 7 e portanto o algarismo 8 não existe nessa base. A
representação 38,3 não existe na base 8.
Conversão de Números da Base 10 para uma Base b
qualquer
A conversão de números da base dez para uma base qualquer emprega algoritmos
que serão o inverso dos acima apresentados. Os algoritmos serão melhor entendidos pelo
exemplo que por uma descrição formal. Vamos a seguir apresentar os algoritmos para a
parte inteira e para a parte fracionária:
Parte Inteira:
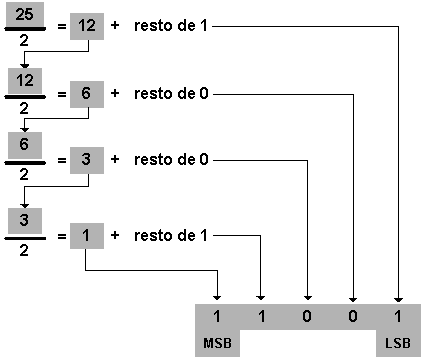
O número decimal será dividido sucessivas vezes pela base; o resto de cada
divisão ocupará sucessivamente as posições de ordem 0, 1, 2 e assim por diante até
que o resto da última divisão (que resulta em quociente zero) ocupe a posição de mais
alta ordem. Veja o exemplo da conversão do número 2510
para a base 2:
Conversão do número (25)10 para a base 2

Experimente fazer a conversão contrária (retornar para a base 10) e ver se o resultado está correto.
Parte Fracionária
Se o número for fracionário, a conversão se fará em duas etapas distintas:
primeiro a parte inteira e depois a parte fracionária. Os algoritmos de conversão são
diferentes. O algoritmo para a parte fracionária consiste de uma série de
multiplicações sucessivas do número fracionário a ser convertido pela base; a parte
inteira do resultado da primeira multiplicação será o valor da primeira casa
fracionária e a parte fracionária será de novo multiplicada pela base; e assim por
diante, até o resultado dar zero ou até encontrarmos o número de casas decimais
desejado. Por exemplo, vamos converter 15,6510 para a
base 2, com 5 e com 10 algarismos fracionários:

Obs.: Em ambos os casos, a conversão foi interrompida quando encontramos o número de algarismos fracionários solicitadas no enunciado. No entanto, como não encontramos resultado 0 em nenhuma das multiplicações, poderíamos continuar efetuando multiplicações indefinidamente até encontrar (se encontrarmos) resultado zero. No caso de interrupção por chegarmos ao número de dígitos especificado sem encontramos resultado zero, o resultado encontrado é aproximado e essa aproximação será função do número de algarismos que calcularmos. Fazendo a conversão inversa, encontraremos:
Com 5 algarismos fracionários:
Parte inteira: 11112 = 1510
Parte fracionária: 0,101002 = 1x2-1 + 0x2-2 + 1x2-3
+ 0x2-4 + 0x2-5 =
0,5 + 0,125 = 0,62510
Com 10 algarismos fracionários:
Parte inteira: 11112 = 1510
Parte fracionária: 0,10100110012 = 1x2-1 + 0x2-2 + 1x2-3
+ 0x2-4 + 0x2-5 +
1x2-6 + 1x2-7 + 0x2-8 + 0x2-9 + 1x2-10
= 1/2 + 1/8 + 1/64 + 1/128 + 1/1024 = 0,5 + 0,125 + 0,015625 + 0,0078125 +
0,0009765625 = 0,649414062510
Ou seja, podemos verificar (sem nenhuma surpresa) que, quanto maior número de algarismos forem considerados, melhor será a aproximação.
Conversão de Números entre duas Bases quaisquer
Para converter números de uma base b para uma outra base b'
quaisquer (isso é, que não sejam os casos particulares anteriormente estudados), o
processo prático utilizado é converter da base b dada para a base 10 e
depois da base 10 para a base b' pedida.
Exemplo: Converter 435 para ( )9.
435 = (4 x 5 + 3)10 = 2310 ==> 23/9 = 2 (resto 5) logo 435
= 2310 = 259