Mapa de Karnaugh

    O Mapa de Karnaugh é uma ferramenta de auxílio à minimização de funções booleanas .  O próprio nome mapa vem do fato dele ser um mapeamento biunívoco a partir de uma tabela-verdade. Vejamos como é feito este mapeamento:

Mapa de  Karnaugh para 1 Variável

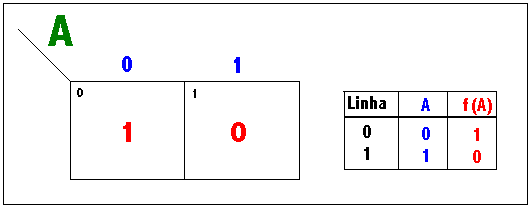
    Considere a tabela-verdade de uma função NOT,

    Para se fazer um Mapa de Karnaugh a partir desta tabela-verdade, realiza-se a construção ilustrada na figura abaixo,

ou seja (veja que a variável A, em verde, está indicando que a função em questão só possui uma variável independente):

Acrescenta-se mais uma coluna à tabela-verdade original. Esta coluna tem por função enumerar as linhas, a partir de zero (0).

Constroi-se tantos quadrículos quantas forem as linhas da tabela-verdade, enumerando-os com o número da linha correspondente no canto superior esquerdo de cada quadrículo (números em preto). Coloca-se os valores das variáveis do lado de fora de cada quadrículo (números em azul).

Coloca-se os valores da função no centro de cada quadrículo, respeitando-se o número da linha correspondente (números em vermelho).

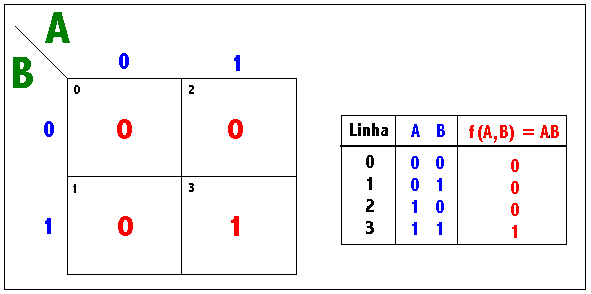
Mapa de Karnaugh para 2 Variáveis

Veja para função de duas varáveis (por exemplo, a função AND),

Mapa de Karnaugh para 3 Variáveis

Para funções de três variáveis independentes,

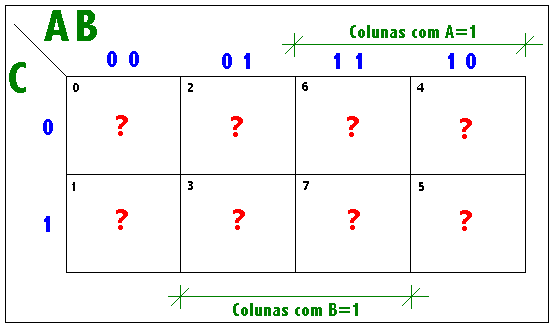
Mapa de Karnaugh para 4 Variáveis

Para funções de quatro variáveis independentes,

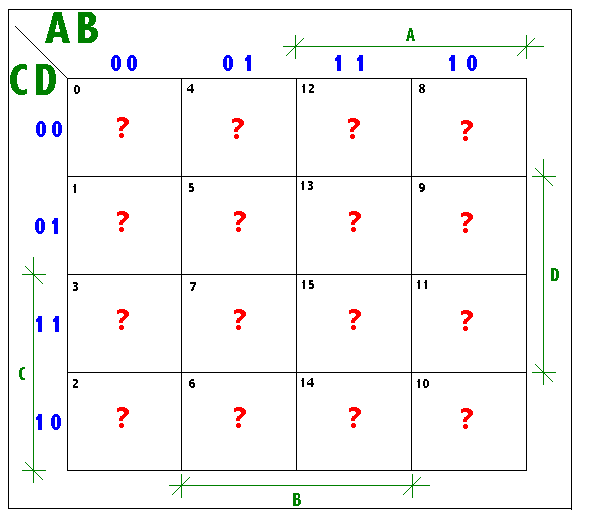
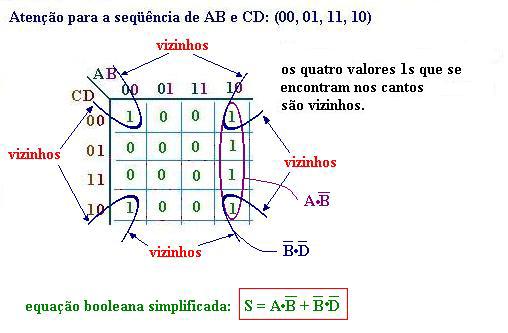
        Note que, a partir do Mapa de Karnaugh para funções três ou mais variáveis independentes, há uma anotação das filas (linhas ou colunas) de quadrículos onde a variável independente não muda de valor. Também observe que, de uma fila de quadrículos para outra fila, só há uma mudança de valor nas variáveis.

        Observe que a ordem de numeração das linhas e colunas, representativas de combinações de variáveis, obedece o código GRAY.

Exemplos de Uso

Ex.1 - Considere a seguinte função lógica de duas variáveis, F(A,B),

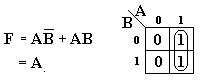
            Do lado da equação booleana, a redução é evidente. Do lado do Mapa de Karnaugh, os dois quadrículos contínuos, contendo o valor lógico 1 cada, indicam que:

A variável A não muda de valor lógico nos dois quadrículos contendo o valor lógico 1 da função F (1 acima da tabela): mantenha a variável A.

A variável B muda de valor lógico nos dois quadrículos contendo o valor lógico 1 da função F (0 e 1 à esquerda da tabela): elimine a variável B.

Ex.2 - Considere, agora, a função de três variáveis, F(A,B,C),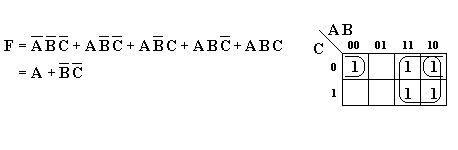

Por não ser trivial a conclusão obtida com o mapa de Karnaugh, aí segue a prova,

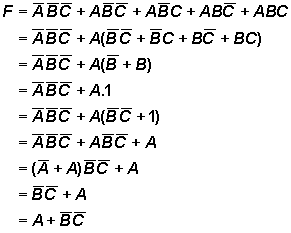
        Como pode ser visto, o mapa de Karnaugh é uma ferramenta eficiente para simplificar funções booleanas.
        Note que no mapa de Karnaugh acima, os quatro quadrículos contíguos: (linha 0 - coluna 11; linha 0 - coluna 10; linha 1 - coluna 11; linha 1 - coluna 10), contendo o valor lógico 1 cada, indicam que a variável A não muda de valor lógico nos quatro quadrículos contendo o valor lógico 1 da função F. Esta é a razão de manter-se a variável A (primeiro termo da simplificação). A variável A muda de valor lógico nos dois quadrículos contendo o valor lógico 1 da função F: elimine a variável A, mantendo B e C complementadas (segundo termo da simplificação).
 

Ex.3 - Considere, agora, a função de quatro variáveis, F(X,Y,Z,W),

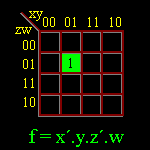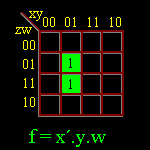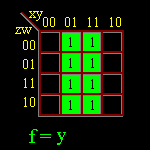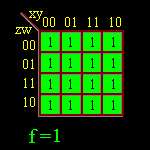
Ex.4 - Desenhar o circuito lógico que possui a tabela verdade a seguir:

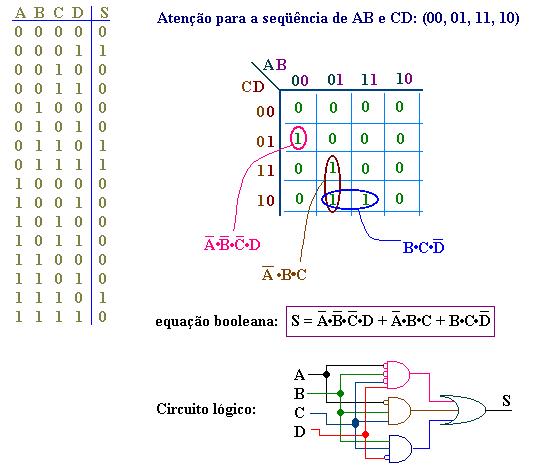
Ex.5 - Obter a equação booleana simplificada para o Mapa de V.Karnaugh a seguir:

| BACK | NEXT |