Variáveis Lógicas

Podemos apenas assumir dois valores quando estamos trabalhando com a Álgebra de BOOLE : nível lógico 0 ou nível lógico 1.

Fig 1 - Alguns exemplos de Variáveis Lógicas.

OBS:

Devido à simplicidade de projeto e construção,os circuitos eletrônicos que formam as máquinas digitais são capazes de distinguir apenas dois níveis de tensão.

Estes sinais elétricos são tensões que assumem dois diferentes valores: um valor de tensão positivo  para representar o nível lógico 1 e um valor aproximado a 0 V (zero volt) para representar o nível lógico 0.

Na realidade, estes valores não são absolutos, e sim faixas de valores, com uma margem de tolerância.


BIT é uma contração de BInary DigiT e representa um dos valores possíveis em binário, 0 ou 1.

BYTE é um grupo de 8 bits.Em um byte, há 2⁸ = 256 combinações, portanto pode-se representar 256 diferentes valores, desde 00000000 até 11111111. O termo "byte" foi inventado pela IBM.

Em informática, a expressão Kilo (abreviada por K) equivale a 2¹⁰, ou seja 1024. Desta forma, 1 Kbit equivale a 2¹⁰ bits, ou seja 1024 bits e Kilobyte (1 KByte) equivale a 2¹⁰ bytes, ou seja 1024 bytes ou ainda 8.192 bits.

Da mesma forma, a expressão Mega equivale a 2²⁰, ou seja 2¹⁰ x 2¹⁰ = 1.048.576. Desta forma, 1 megabit (1 Mbit) equivale a 2²⁰ bits, ou seja 1024 Kbits ou 1.048.576 bits e 1 Megabyte equivale a 2²⁰ bytes, ou seja 1.048.576 bytes.

A Álgebra de BOOLE possui apenas três operações básicas:

1. Lógica OU, também chamada função lógica OR. O símbolo utilizado é +
2. Lógica E, também chamada função lógica AND. O símbolo utilizado  é .
3. Complementação Lógica, ou inversão, também chamada de função lógica NOT. A barra sobreposta ( ^- ) é o simbolo utilizado para indicar esta função.

Função Lógica OR

A	B	X = A + B	SIMBOLOGIA
0	0	0
0	1	1
1	0	1
1	1	1

Fig 2 - Tabela-verdade da função lógica OR  e Simbologia.

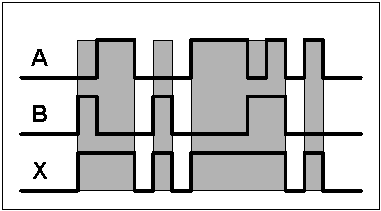
Fig 3 - Diagramas de tempo para Porta Lógica OR.

            A porta lógica OR opera de tal maneira que a saída estará no nível lógico ALTO se uma das entradas ou ambas simultaneamente estiverem no nível lógico ALTO. A saída estará no nível lógico BAIXO se todas as entradas estiverem no nível lógico BAIXO.

Função Lógica AND

A	B	X = A . B	SIMBOLOGIA
0	0	0
0	1	0
1	0	0
1	1	1

Fig 4 - Tabela-verdade da operação lógica AND  e Simbologia.

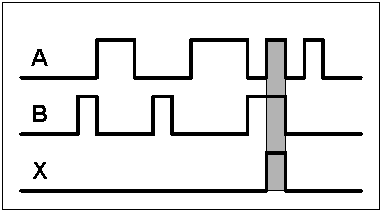
Fig 5 - Diagramas de tempo para Porta Lógica AND.

A porta lógica AND opera de tal maneira que a saída estará no nível lógico ALTO sempre que todas as entradas estiverem no nível lógico ALTO. A saída estará no nível lógico BAIXO se qualquer uma das entradas estiver no nível lógico BAIXO.

 

---

Função Lógica NOT

---

A	X = A'	SIMBOLOGIA
0	1
1	0

Fig 6- Tabela-verdade da operação lógica NOT e Simbologia.

A Porta NOT ou de negação atua sobre uma única variável de entrada, ao contrário das operações AND e OR vistas até agora.

OBS:  Será utilizado o simbolo (') para representar a inversão.

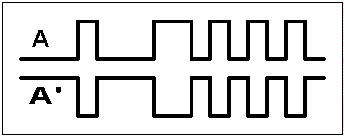
Fig 7 - Diagramas de tempo para Porta Lógica NOT

Operação Algébrica para Circuitos Lógicos

Um circuito lógico, por mais trabalhoso que seja, pode ser implementado através das operações básicas, AND, OR ou NOT.

Deve-se tomar cuidado com a expressão booleana na hora de determinar qual o membro que será trabalhado inicialmente, observe o exemplo a seguir :

S = A . B + C

Utilizaremos a mesma regra determinada pela álgebra comum, primeiramente a multiplicação lógica, para depois efetuarmos a soma lógica. Veja a tabela verdade a seguir:

Observe que o resultado é diferente. ATENÇÃO!!!

Obtenção da Função lógica da saída a partir de Circuitos Lógicos

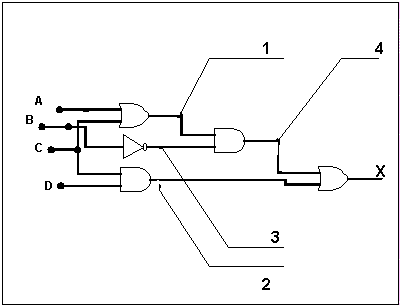
    1. A + C

    2. C.D

    3. B'

    4. ( A+C).B'

Então temos : X = (C . D) + [(A + C) . B']

Implementação de Circuitos Lógicos a partir de uma Função lógica de saída

Conhecendo-se a expressão lógica que define a função de um circuito, podemos construí-lo a partir desta expressão. Por     exemplo, se necessitamos de um circuito definido como X= A . B . C, saberemos logo como construí-lo, pois, pela expressão fica claro que uma porta AND de três entradas é a solução. Se a operação for  X= A + B', uma porta OR com NOT em uma das entradas resolve a questão. O mesmo raciocínio poder ser empregado na construção de circuitos lógicos de maior complexidade.

Observe a seguinte expressão: x = (A + B)' . C + (A' . C').(A + B'). Veja  o  circuito a seguir:

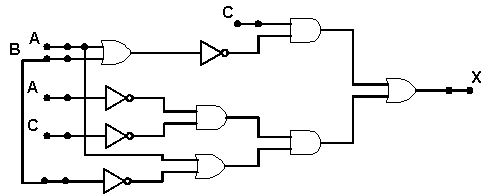
Veja outro exemplo:

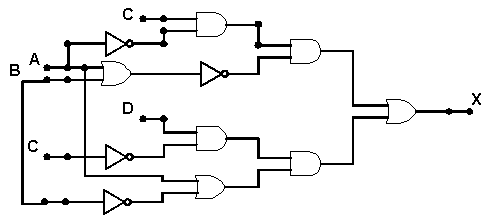
X = (C . A') . (A + B)' + (D . C') . (A + B')

Portas Lógicas NAND e NOR

A	B	X = (A . B)'	SIMBOLOGIA
0	0	1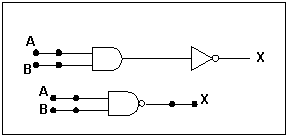
0	1	1
1	0	1
1	1	0

Fig 8 - Tabela-verdade da função lógica NAND e Simbologia.

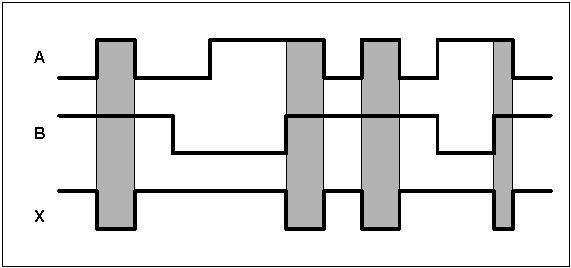
Fig 9 - Diagramas de tempo para Porta Lógica NAND.

A	B	X = (A + B)'	SIMBOLOGIA
0	0	1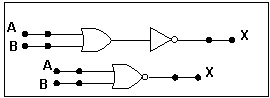
0	1	0
1	0	0
1	1	0

Fig 10 - Tabela-verdade da função lógica NOR  e Simbologia.

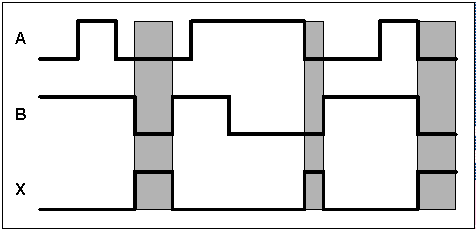
Fig 11 - Diagramas de tempo para Porta Lógica NOR.

É possível implementar qualquer função lógica, utilizando-se somente portas NAND ou NOR, sem nenhuma outra porta lógica. Veja os exemplos abaixo:

PORTAS LÓGICAS
Porta Lógica NOT	Implementado com Porta Lógica NOR	Implementado com Porta Lógica NAND
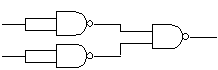
Porta Lógica AND	Implementado com Porta Lógica NOR	Implementado com Porta Lógica NAND
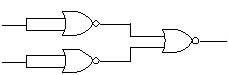
Porta Lógica OR	Implementado com Porta Lógica NOR	Implementado com Porta Lógica NAND

Como qualquer funçaõ lógica pode ser implementada usando-se apenas portas NAND, conseqüentemente qualquer circuito lógico pode ser construído só com portas NAND. A mesma conclusão é válida para portas NOR. Estas características das portas NAND e NOR podem ser muito úteis no projeto e desenvolvimento de circuitos lógicos.

BACK